Funciones polinómicas
Una función polinomial es una función algebraica cuya estructura cumplen con la definición de polinomio, esto es, $$P\left(x\right)=a_nx^n+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\cdots+ax+a_0$$ donde todos los exponentes de la variable \(x\) son no negativos. El estudio de las funciones polinomiales se inicia con las funciones lineales también llamadas funciones afines por algunos autores, por ser el más simple de los casos.
Funciones lineales.
Es común en ciencia y en economía encontrar diversos modelos matemáticos escrito como funciones lineales, en física se encuentran varias funciones lineales importantes como son \(x=vt+x_0\) ecuación posición para movimiento rectilíneo con velocidad constante, \(F=ma\) para la magnitud de la fuerza ejercida sobre una partícula que posee masa constante, entre otras muchas otras las cuales se irán estudiando en el paso de este curso y otras en cursos superiores.
Una función lineal se expresa en la forma \(y=mx+n\) que en notación de función es \(f\left(x\right)=mx+n\) dónde los números \(m\) y \(n\in\mathbb{R},\) ye es llamada variable dependiente y \(x\) es la variable independiente. Las variables \(x\) y ye son lineales (exponente uno), y la principal característica de esta función es que su gráfica es una línea recta, por esto el nombre de “lineal”. El número \(n\) es llamado la ordenada en el origen porque la función corta el eje vertical en el punto \((0,n),\) este representa el valor de \(y=f(x)\) para \(x=0\) es decir \(y(0).\) En cuanto a la pendiente \(m\) ésta se define como
Definición de pendiente de una recta no vertical.
Sea la recta \(y=mx+n\) una recta no vertical cualquiera, la pendiente \(m\) de la recta, es la tangente de su ángulo de inclinación \(\phi\) con el eje horizontal, dada por:
$$m=\tan{\phi} =\frac{∆y}{∆x}=\frac{y_2-y_1}{x_2-x_1}~~~~~\mathrm{donde}~~x_2≠x_1$$
Ejemplo 1. Determine la pendiente de la recta que pasa por los puntos \((2,\ 4)\) y \((6,\ 8).\)
Solución: se inicia identificando los puntos \(P_1=(2,\ 4)=(x_1,\ y_1)\) y \(P_2=(6,\ 8)=(x_2,\ y_2)\) para luego sustituir estos valores en la expresión,
$$m=\frac{y_2-y_1}{x_2-x_1}=\frac{8-4}{6-2}=\frac{4}{4}=1$$
¿Qué pasaría si se intercambian los puntos \(P_1\) y \(P_2\) y se realizan los cálculos nuevamente? Se encuentra que la pendiente no cambia, de modo que no importa cual punto sea etiquetado como \((x_1,\ y_1)\) o \((x_2,\ y_2)\) lo importante, es recordar que \(x_1,\) va junto a \(y_1;\) \(x_2\) junto a \(y_2.\)
Ejemplo 2. Determine el valor \(x\) para que la pendiente entre los puntos \((3,5)\) y \((x,\ 7)\) sea 2.
Solución: aplicando la definición de pendiente para los puntos dados,
$$2=\frac{7-5}{x-3}\ \Longrightarrow\ 2\left(x-3\right)=2\Leftrightarrow2x-6=2\Longrightarrow x=4$$
Evaluando funciones lineales
Evaluar una función lineal en un valor determinado, al igual que cuando se evalúa cualquier otra función, es encontrar el valor de dicha función al sustituir la variable independiente por un valor dado, tal y como se hizo al evaluar funciones.
Ejemplo 3. Evaluar la función \(f(x)=5x+13\) en \(x=3; x=1/5\) y \(x=0\)
Solución: sustituyendo en la función cada uno de los valores dados por \(x\) se tiene,
\begin{array}{l}
f(3)=5(3)+13=15+13=28\\
f\left(\frac15\right)=5\left(\frac15\right)+13=14\\
f(0)=5(0)+13=13\end{array}
Ejemplo 4. Evaluar la función \(y=7x+11\) para \(x=0~~~~x=1/7\) y \(x=5/14.\)
Solución: sustituyendo cada uno de los valores dados por \(x\) en la función,
\begin{array}{l}
y(0)=7(0)+11=11\\
y\left(\frac17\right)=7\left(\frac17\right)+11=12\\
y\left(\frac{5}{14}\right)=7\left(\frac5{14}\right)+11=\frac{27}{2}\\
\end{array}
Como puede notar de los ejemplos tres y cuatro, evaluar \(y(0)=n\) como era de esperarse.
Para más contenidos clic en y luego clic en la pestaña del contenido deseado.
Graficando funciones lineales.
Para graficar una función cualquiera, se requiere en primer lugar estudiar el plano cartesiano y algunas de sus propiedades.
El plano cartesiano es un sistema coordenado rectangular (que forma un rectángulo), formado por dos rectas numéricas que se intersecan perpendicularmente en un punto llamado origen, correspondiente al punto cero de cada una de las rectas, mediante un sistema de coordenadas.
Las rectas numéricas horizontal y vertical son llamadas ejes de abscisas (usualmente el eje \(x\) y eje de ordenadas (usualmente eje \(y\)).
Los dos ejes dividen al plano en cuatro regiones llamadas cuadrantes, y no necesariamente deben tener la misma escala al ser dibujados.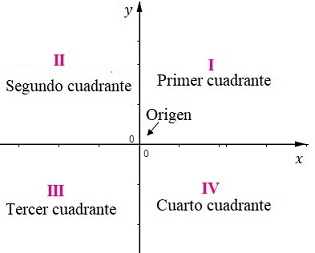 
El plano que queda determinado por los ejes recibe el nombre de plano \(xy\) y permite unir dos de las ramas más importante de la Matemática, el álgebra y la geometría, las cuales siembran las bases para el estudio de otras ramas como son la trigonometría y el cálculo.
Sea \(P\) un punto en el plano cartesiano, ubicado en cualquiera de los cuadrantes. Se asocia un par ordenado (pareja de números reales que tienen un orden) al punto \(P\) al trazar una recta vertical desde \(P\) al eje de abscisas (eje \(x\)) y una recta horizontal desde \(P\) al eje de ordenadas (eje \(y\).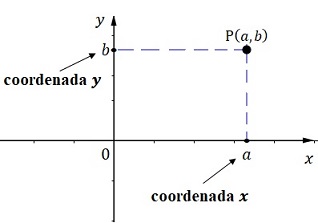 
Si la recta vertical corta el eje de abscisas en \(x=a\) y la recta horizontal corta el eje de ordenada en \(y=b\), el par ordenado de números reales asociado al punto \(P\) es \(P\left(a,b\right)\), el número a es la abscisa o coordenada en \(x\) del punto y el número \(b\) es la ordenada o coordenada en \(y\). Recuerde que las letras no importan, puede representar el par ordenado como \(\left(x,y\right)\) o \(\left(h,k\right)\) según guste.
Por convención se ha establecido que a la derecha y arriba del origen de coordenadas, punto \((0,0)\) es positivo, mientras que a la izquierda y abajo se considera negativo como puede verse en la figura de la izquierda.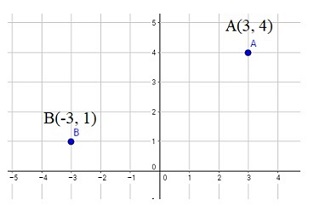
Así el punto \(\left(3,4\right)\) quiere decir tres unidades (lugares) a la derecha del \(\left(0,0\right)\) y luego cuatro unidades hacia arriba. Para el punto \(\left(-3,1\right)\) se deben considerar tres unidades a la izquierda del origen \(\left(0,0\right)\) y luego una unidad hacia arriba, como puede verse en la figura.
Gráfica de una función.
Dada una función cualquiera \(y=f\left(x\right)\) la gráfica de dicha función es el conjunto de puntos \(\left(x,y\right)\) del plano cartesiano que cumplen la condición dada por la función. La gráfica de una función brinda información de su comportamiento para ciertos valores de la variable independiente.
A menudo es necesario realizar gráficas de funciones constante como \(x=h\) o \(y=k\) donde \(h\) y \(k\) son números reales cualesquiera. Las gráficas de estás funciones son la línea recta vertical \(x=h\) y la línea recta horizontal \(y=k\) a continuación, se presentan dos ejemplos de gráficas de estas funciones. Note de la figura a, que sin importar el valor ye \(x\) siempre es igual a \(h,\) mientras que en la figura \(b,\) sin importar el valor de \(x,\) \(y=k\) por esta razón es que se les llaman funciones constantes.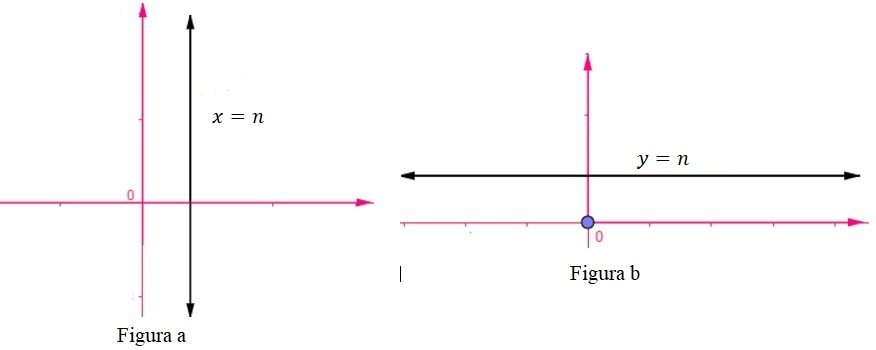
Para graficar una función lineal basta conocer dos puntos por donde pasa la función \(y=mx+n\), y unirlos con una línea recta. Como ya se sabe \(y=mx+n\) pasa por \((0,n)\), para el otro punto, se hace \(x\) igual a cualquier valor y se evalúa la función.
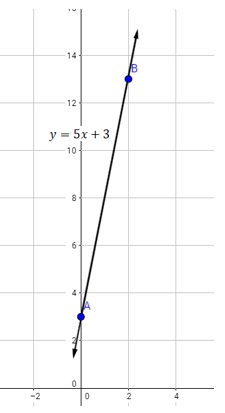Ejemplo. Graficar la función \(y=5x+3\).
Solución: se necesitan al menos dos puntos para graficar una recta, la recta dada pasa por \((0,n)=(0,3)\) para el otro punto evaluar \(y=5x+3\) en otro valor, por ejemplo \(y(2)=5(2)+3=13\) de donde se tiene \((2,\ 13)\). Ahora ubique los puntos encontrados \(A(0,3)\) y \(B(2,\ 13)\) en el plano cartesiano, y luego únalo con una línea recta.
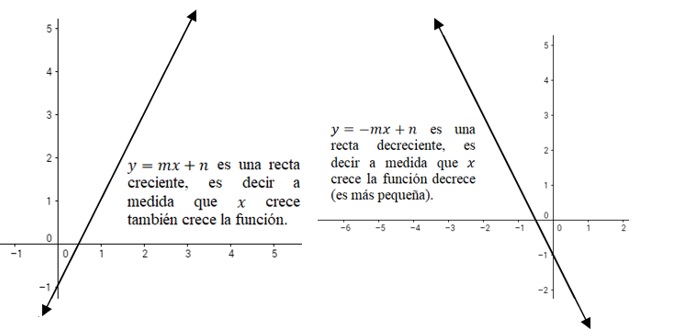
A continuación, se presentan las gráficas de las funciones lineales \(y=mx+n\) junto con la de \(y=-mx+n\) con la intensión de observar lo que sucede para \(\pm m\). Una característica importante de las gráficas de funciones lineales, si \(m\) es positivo, la recta es creciente siempre, y si \(m\) es negativo, la recta es decreciente siempre, más adelante al estudiar geometría analítica podrá analizar con mayor profundidad este hecho.
Para más contenidos y luego clic en la pestaña del contenido deseado.
Modelación con funciones lineales.
Para la modelación matemática mediante las funciones lineales, es necesario el conocimiento de la parte introductoria de geometría analítica llamada “ecuaciones de la recta” a continuación se presentan algunos de estos resultados sin entrar en los detalles de las demostraciones.
Como ya se ha dicho en la expresión \(y=mx+n\) el número real \(m\) representa un valor de gran importancia llamado “pendiente” el cual mide la inclinación de la recta con el eje horizontal, por tal razón los matemáticos también le llaman “coeficiente angular” y el número \(n\) es el valor de la función en el momento inicial \((x=0\) o \(t=0)\). La definición de pendiente es como sigue.
Definición de pendiente de una recta no vertical.
Sea la recta \(y=mx+n\) una recta no vertical cualquiera, la pendiente \(m\) de la recta, es la tangente de su ángulo de inclinación \(\theta\) con el eje horizontal, dada por:
$$m=\tan{\theta}=\frac{∆y}{∆x}=\frac{y_2-y_1}{x_2-x_1}~~{\rm donde}~~ x_2≠x_1$$
Esta es interpretada como la razón de cambio o tasa a la cual está cambiando el objeto de estudio, con relación a la variable en que se está midiendo.
Ejemplo 1. Determine la pendiente de la recta que pasa por los puntos \(\left(2,4\right)\) y \(\left(6, 8\right)\).
Solcuión: comience por identificar los puntos \(P_1=\left(2,\ 4\right)=\left(x_1,\ y_1\right)\) y \(P_2=\left(6,\ 8\right)=\left(x_2,\ y_2\right)\)
$$m=\frac{y_2-y_1}{x_2-x_1}=\frac{8-4}{6-2}=\frac{4}{4}=1$$
Intercambie los puntos \(P_1\) y \(P_2\) y determine nuevamente la pendiente ¿Qué puede concluir del resultado? Los resultados son iguales.
Ecuaciones de la recta.
Aunque matemáticamente no existe una definición de recta, una idea conceptual de recta es “un conjunto de puntos sucesivos sobre una misma línea, que se extiende al infinito por ambos lados” los puntos en que una recta interseca (corta) los ejes de abscisa y ordenada se llaman interceptos y se representan con los puntos \(\left(a,0\right)\) para el eje de abscisa (eje horizontal) y para el eje de ordenada (eje vertical) el punto \(\left(0,n\right)\). Según la inclinación de una recta su ecuación puede tomar una o más de las siguientes formas:
Ecuaciones de la recta
\begin{array}{l l}
{\rm ~~~~~~~~~~~~~Forma}& {\rm Ecuación}\\ \hline
{\rm Recta ~horizontal},~m=0& x=h\\
{\rm Recta~vertical}, m=∞~~ {\rm (indefinida)}& y=k\\
{\rm Pendiente~intercepto~pasa~por~}(0,n)&y=mx+n\\
{\rm Punto~pendiente~pasa~por~}(x_1,y_1)&y=m(x-x_1)+y_1\\
{\rm Forma~general,}~~m=-a/b&ax+by+c=0\end{array}
Ejemplo 3: Determine la ecuación de la recta que pasa por los puntos \(\left(2, 3\right)\) y \(\left(4, -2\right)\)
Solución: comience por determinar la pendiente de la recta.
$$m=\frac{∆y}{∆x}=\frac{y_2-y_1}{x_2-x_1}⟹m=\frac{-2-3}{4-2}⟹m=-\frac52$$
Usando ahora la ecuación punto pendiente \(y=m\left(x-x_1\right)+y_1~~\) para \(m=-\frac{5}{2}\) y el punto \(\left(2,\ 3\right)\),
\begin{align}
&y=-\frac{5}{2}\left(x-2\right)+3\\
&2y=-5(x-2)+6\\
&2y=-5x+10+6\\
&5x+2y-16=0\end{align}
¿Qué pasaría si se utiliza \(m=-\frac{5}{2}\) y el punto \(\left(4,-2\right)\)? El resultado sería el mismo.
Ejemplo 4. Determine la ecuación de la recta que pasa por \(\left(0, 6\right)\) y su pendiente \(m=2\).
Solución: la pendiente es \(m=2\), como pasa por \(\left(0,6\right)\) se tiene el intercepto, por tanto, se tienen los elementos para la forma pendiente intercepto \(y=mx+n\).
$$\left(0,6\right)=\left(0,n\right)\Longleftrightarrow\ n=6;\ \ \ m=2\ \ para\ \ y=mx+n\Longrightarrow\ y=2x+6$$
Suponga usted que no recuerda la forma pendiente intercepto y usa la forma \(y-y_1=m\left(x-x_1\right)\Longrightarrow y-6=2\left(x-0\right)\Longrightarrow y=2x+6\) que es el resultado anterior.
Ejemplo 5. Determinar la ecuación de la recta que cuya pendiente \(m=0\) y pasa por el punto \(\left(4, 7\right)\).
Solución: para \(y=mx+n\) si \(m=0\) se tiene una recta horizontal \(y=k\). Una recta horizontal que pasa por \(\left(4,\ 7\right)\) es la recta pasa por \(y=7\)
Para más contenidos clic en y luego clic en la pestaña del contenido deseado.
Determina la pendiente de la pendiente de la recta que pasa por los puntos: \begin{align} 1.&~A(2,\ 3)~~ y~~B(-2,4)\\ 2.&~A(4,\ 5)~~y~~B\left(3,\ 8\right)\\ 3.&~A\left(\frac{1}{2},~~\frac{3}{4}\right)~~y~~B\left(\frac{6}{4},~~\frac{9}{8}\right) \end{align}
Determine la ecuación de la recta que cumple las condiciones establecidas.
\(1.\) Pasa por \(\left(0,\ 6\right)\) y su pendiente \(m=2.\)
\(2.\) Tienes pendiente \(m=0\) y pasa por el punto \(\left(4,\ 7\right).\)
\(3.\) Pasa por los puntos \((2,-4)\) y \((5,2)\)
\(4.\) Pasa por los puntos \((6,-4)\) y \((-3,-10)\) y se pide escribir su ecuación general.
Un taxista de cierta compañía cobra \($150\) por parar y subir los pasajeros y luego \($30\) por cada kilómetro recorrido.
a) Determine la función lineal que relacione la tarifa y los kilometro recorridos.
b) ¿Cuánto debe pagar una persona que recorre \(20km\)?
El costo por la tarifa por el servicio de una empresa telefónica está dada por la expresión \(C(t)=1.5t+400\), donde \(t\) es la cantidad de minutos consumidos mensualmente.
\(a.\) Describa de manera escrita cómo funciona la tarifa.
\(b.\) ¿Cuánto pagará una persona que consume \(300\) minutos en un mes?
\(c.\) Si una persona pagó una factura de \($775\) ¿cuántos minutos consumió en el mes?
El dos de enero de cierto año se compró una máquina por \($500 000\) la cual se deprecia linealmente. Si al cabo de diez años el valor de la máquina es de \($85 000.\)
\(a.\) Encuentre una función que exprese el valor \(V\) de la máquina con respecto del tiempo \(t\), suponiendo una relación lineal.
\(b.\) Determine el valor de la máquina a los siete años de comprada.
\(c.\) ¿En qué tiempo el valor de la máquina es cero para fines de inventario?
\(d.\) realice un boceto a escala de la gráfica de la función.
Para efectos tributarios un computador personal se deprecia linealmente hasta llegar a cero en diez años. Si el valor de compra de un computador fue \($50 000.\)
\(a.\) Determine una función lineal que exprese el valor del computador como una función del tiempo.
\(b.\) Realice un boceto a escala de la gráfica de la función.
Desde el comienzo del año el precio de la gasolina regular ha aumentado a una tasa constante de \($5.00\) por galones al mes. Si al treinta de junio el precio había llegado a \($225.00\) por galón.Determine una función que exprese el precio como función del tiempo y dibuje un boceto a escala de su gráfica.
Suponga que el costo total de producir 10 unidades de cierto producto en una industria es \($400\) mientras que el de 20 unidades es \($650.\) Si el costo \(C\) está relacionado linealmente con la cantidad a producir \(q\).
\(a.\) Determine una función lineal que relacione el costo con la cantidad a producir.
\(b.\) Determine el costo fijo y variable de la producción.
\(c.\) Determine el costo de producir 1025 unidades.
En una compañía un empleado recién contratado cobra \($15 000\) y un empleado con cinco años de antigüedad cobra \($25 000\)
\(a.\) Determinar la ecuación del sueldo como función del tiempo, suponiendo que la relación es lineal.
\(b.\) ¿Cuánto cobra un empleado que tiene diez años en la empresa?
\(c.\) ¿Qué tiempo tiene en la empresa tiene una persona que cobra \($42 000\)?
Bajo ciertas condiciones el agua alcanza su punto de solidificación una temperatura de cero grados Celcius unos treinta y dos grados Fahrenheit y su punto de ebullición a 100 grados Celsius unos 212 grados Fahrenheit.
\(a.\) Suponiendo una relación lineal entre las dos temperaturas, determine la función lineal que expresa la temperatura Fahrenheit como función de Celsius.
\(b.\) Use la función encontrada para convertir la temperatura corporal de grados Celsius a grados Fahrenheit.
\(c.\) Si una temperatura corporal de 103 grados Fahrenheit representa un peligro eminente para una persona que puede causar daños neurológicos, determine la temperatura corporal en grados Celsius a la que esto ocurre, a partir de relación enontrada.